| 1 |
dashley |
3 |
%$Header: /home/dashley/cvsrep/e3ft_gpl01/e3ft_gpl01/dtaipubs/esrgubka/c_bal0/c_bal0.tex,v 1.10 2003/11/03 02:14:24 dtashley Exp $
|
| 2 |
|
|
|
| 3 |
|
|
\chapter[\cbalzeroshorttitle{}]{\cbalzerolongtitle{}}
|
| 4 |
|
|
|
| 5 |
|
|
\label{cbal0}
|
| 6 |
|
|
|
| 7 |
|
|
\section{Introduction, Definition, And History Of Boolean Algebra}
|
| 8 |
|
|
%Section tag: INT0
|
| 9 |
|
|
\label{cbal0:sint0}
|
| 10 |
|
|
|
| 11 |
|
|
\index{Boolean algebra}
|
| 12 |
|
|
In this chapter, we review methods of
|
| 13 |
|
|
simplifying \index{Boolean function}Boolean functions, and
|
| 14 |
|
|
show how such methods can be used to simplify software constructs
|
| 15 |
|
|
or to construct software which is more compact (in ROM or RAM)
|
| 16 |
|
|
or executes more quicky.
|
| 17 |
|
|
|
| 18 |
|
|
Boolean algebra is named after \index{Boole, George}George Boole,
|
| 19 |
|
|
a 19th-century British mathematician.
|
| 20 |
|
|
A fairly concise biography of George Boole comes from
|
| 21 |
|
|
\cite{bibref:w:georgeboolebio01}:
|
| 22 |
|
|
|
| 23 |
|
|
\begin{quote}
|
| 24 |
|
|
George Boole first attended a school in Lincoln, then a commerical school.
|
| 25 |
|
|
His early instruction in mathematics, however, was from his father who
|
| 26 |
|
|
also gave George a liking for constructing optical instruments. George's
|
| 27 |
|
|
interests turned to languages and he received instruction in Latin from a
|
| 28 |
|
|
local bookseller.
|
| 29 |
|
|
|
| 30 |
|
|
By the age of 12 George had become so skilled in Latin that it provoked
|
| 31 |
|
|
an argument. He translated an ode by the Latin poet Horace which his
|
| 32 |
|
|
father was so proud of that he had it published. However the talent was
|
| 33 |
|
|
such that a local schoolmaster disputed that any 12 year old could
|
| 34 |
|
|
have written with such depth.
|
| 35 |
|
|
|
| 36 |
|
|
Boole did not study for an academic degree, but from the age of 16 he was an
|
| 37 |
|
|
assistant school teacher. He maintained his interest in languages
|
| 38 |
|
|
and intended to enter the Church. From 1835, however, he seems to have
|
| 39 |
|
|
changed his mind for he opened his own school and began to study mathematics
|
| 40 |
|
|
on his own. He was later to realize that he had almost wasted five years
|
| 41 |
|
|
in trying to teach himself the subject instead of having a skilled teacher.
|
| 42 |
|
|
|
| 43 |
|
|
At this time Boole studied the works of Laplace and Lagrange, making
|
| 44 |
|
|
notes which would later be the basis for his first mathematics paper.
|
| 45 |
|
|
However he did receive encouragement from Duncan Gregory who at this
|
| 46 |
|
|
time was in Cambridge and the editor of the recently founded
|
| 47 |
|
|
\emph{Cambridge Mathematical Journal}.
|
| 48 |
|
|
|
| 49 |
|
|
Boole was unable to take Duncan Gregory's advice and study courses at
|
| 50 |
|
|
Cambridge as he required the income from his school to look after
|
| 51 |
|
|
his parents. However he began publishing in the \emph{Cambridge
|
| 52 |
|
|
Mathematical Journal} and his interests were also influenced by Duncan Gregory
|
| 53 |
|
|
as he began to study algebra. An application of algebraic methods
|
| 54 |
|
|
to the solution of differential equations was published by Boole in the
|
| 55 |
|
|
\emph{Transactions of the Royal Society} and for this work he received
|
| 56 |
|
|
the Society's Royal Medal. His mathematical work was beginning to bring
|
| 57 |
|
|
him fame.
|
| 58 |
|
|
|
| 59 |
|
|
Boole was appointed to the chair of mathematics at Queens College,
|
| 60 |
|
|
Cork in 1849. He taught there for the rest of his life, gaining a reputation
|
| 61 |
|
|
as an outstanding and dedicated teacher.
|
| 62 |
|
|
|
| 63 |
|
|
In 1854 he published \emph{An investigation into the Laws of Thought, on
|
| 64 |
|
|
Which are founded the Mathematical Theories of Logic and Probabilities}.
|
| 65 |
|
|
Boole approached logic in a new way reducing it to a simple algebra,
|
| 66 |
|
|
incorporating logic into mathematics. He pointed out the analogy
|
| 67 |
|
|
between algebraic symbols and those that represent logical forms.
|
| 68 |
|
|
It began the algebra of logic called Boolean algebra which now finds
|
| 69 |
|
|
application in computer construction, switching circuits etc.
|
| 70 |
|
|
|
| 71 |
|
|
Boole also worked on differential equations, the influential
|
| 72 |
|
|
\emph{Treatise on Differential Equations} appeared in 1859, the calculus of finite
|
| 73 |
|
|
differences, \emph{Treatise on the Calculus of Finite Differences} (1860),
|
| 74 |
|
|
and general methods in probability. He published around 50 papers and
|
| 75 |
|
|
was one of the first to investigate the basic properties of numbers, such
|
| 76 |
|
|
as the distributive property, that underlie the subject of algebra.
|
| 77 |
|
|
|
| 78 |
|
|
Many honours were given to Boole as the genius in his work was recognised.
|
| 79 |
|
|
He received honorary degrees from the universities of Dublin
|
| 80 |
|
|
and Oxford and was elected a Fellow of the Royal Society (1857).
|
| 81 |
|
|
However his career, which was started rather late, came to an unfortunately
|
| 82 |
|
|
early end when he died at the age of 49. The circumstances are described
|
| 83 |
|
|
by Macfarlane in [17]\footnote{As reproduced from
|
| 84 |
|
|
\cite{bibref:w:georgeboolebio01}---this is not a valid reference
|
| 85 |
|
|
number in this work.} as follows:
|
| 86 |
|
|
|
| 87 |
|
|
\begin{quote}
|
| 88 |
|
|
One day in 1864 he walked from his residence to the College,
|
| 89 |
|
|
a distance of two miles, in the drenching rain, and lectured in wet
|
| 90 |
|
|
clothes. The result was a feverish cold which soon fell upon his
|
| 91 |
|
|
lungs and terminated his career \ldots{}
|
| 92 |
|
|
\end{quote}
|
| 93 |
|
|
|
| 94 |
|
|
What Macfarlane fails to say is that Boole's wife
|
| 95 |
|
|
(Mary---niece of Sir George Everest, after whom the mountain is named) believed that a
|
| 96 |
|
|
remedy should resemble the cause. She put Boole to bed and threw
|
| 97 |
|
|
buckets of water over the bed since his illness had been caused by getting
|
| 98 |
|
|
wet.
|
| 99 |
|
|
|
| 100 |
|
|
Hirst described Boole as:
|
| 101 |
|
|
|
| 102 |
|
|
\begin{quote}
|
| 103 |
|
|
\ldots{} evidently an earnest able and at the same time a genial man.
|
| 104 |
|
|
\end{quote}
|
| 105 |
|
|
|
| 106 |
|
|
His work was praised by \index{DeMorgan, Augustus}De Morgan who said:
|
| 107 |
|
|
|
| 108 |
|
|
\begin{quote}
|
| 109 |
|
|
Boole's system of logic is but one of many proofs of genius and patience combined.
|
| 110 |
|
|
\ldots{} That the symbolic processes of algebra,
|
| 111 |
|
|
invented as tools of numerical calculation, should be competent to
|
| 112 |
|
|
express every act of thought, and to furnish the grammar and
|
| 113 |
|
|
dictionary of an all-containing system of logic, would not have
|
| 114 |
|
|
been believed until it was proved. When Hobbes \ldots{} published his
|
| 115 |
|
|
``Computation or Logique'' he had a remote glimpse of some of the points which
|
| 116 |
|
|
are placed in the light of day by Mr Boole.
|
| 117 |
|
|
\end{quote}
|
| 118 |
|
|
|
| 119 |
|
|
Boolean algebra has wide applications in telephone switching and the
|
| 120 |
|
|
design of modern computers. Boole's work has to be seen as a
|
| 121 |
|
|
fundamental step in today's computer revolution.
|
| 122 |
|
|
(Article by: J. J. O'Connor and E. F. Robertson.)
|
| 123 |
|
|
\end{quote}
|
| 124 |
|
|
|
| 125 |
|
|
In the preface of
|
| 126 |
|
|
\cite{bibref:b:whitesittbooleanalgandapps}, Whitesitt explains the
|
| 127 |
|
|
significance of Boole's work:
|
| 128 |
|
|
|
| 129 |
|
|
\begin{quote}
|
| 130 |
|
|
George Boole (1815-1864) introduced in his book \emph{The Laws Of Thought}
|
| 131 |
|
|
the first systematic treatment of logic and developed for this purpose
|
| 132 |
|
|
the algebraic system now known by his name, Boolean algebra. Few
|
| 133 |
|
|
mathematical works of the last 100 years have had a greater impact
|
| 134 |
|
|
upon mathematics and philosophy than this famous book. The significance
|
| 135 |
|
|
of the work has been well expressed by Augustus De Morgan:
|
| 136 |
|
|
|
| 137 |
|
|
\begin{quote}
|
| 138 |
|
|
That the symbolic processes of algebra, invented as tools of numerical
|
| 139 |
|
|
calculation, should be competent to express every act of thought, and to
|
| 140 |
|
|
furnish the grammar and dictionary of an all-containing system of
|
| 141 |
|
|
logic, would not have been believed until it was proved in
|
| 142 |
|
|
\emph{Laws Of Thought}.
|
| 143 |
|
|
\end{quote}
|
| 144 |
|
|
|
| 145 |
|
|
In addition to its applications in the field of logic, Boolean algebra
|
| 146 |
|
|
has two other important applications. The first of these arises from
|
| 147 |
|
|
the fact that Boolean algebra is the natural algebra with which to
|
| 148 |
|
|
treat the combination of sets of elements under the operations of
|
| 149 |
|
|
intersection and union of sets. With the addition of the idea of
|
| 150 |
|
|
``number of elements'' in a set, Boolean algebra becomes the
|
| 151 |
|
|
foundation for the theory of probability. The algebra
|
| 152 |
|
|
of sets is also important in many other branches of mathematics.
|
| 153 |
|
|
|
| 154 |
|
|
With the publication of two papers approximately 20 years
|
| 155 |
|
|
ago,\footnote{Whitesitt's book was first published in 1961,
|
| 156 |
|
|
so Whitesitt probably means \emph{20 years ago} with
|
| 157 |
|
|
respect to 1961.}
|
| 158 |
|
|
\index{Shannon, Claude E.}Claude E. Shannon introduced a new
|
| 159 |
|
|
area of application of
|
| 160 |
|
|
Boolean algebra when he showed that the basic properties of
|
| 161 |
|
|
series and parallel combinations of bistable electrical
|
| 162 |
|
|
devices such as relays could be adequately represented
|
| 163 |
|
|
by this algebra. Since this time, Boolean algebra has
|
| 164 |
|
|
played a significant role in the important and complicated
|
| 165 |
|
|
task of designing telephone switching circuits, automatic
|
| 166 |
|
|
control devices, and electronic computers. At the present
|
| 167 |
|
|
time, more interest is centered in this application than
|
| 168 |
|
|
in either of the others.
|
| 169 |
|
|
\end{quote}
|
| 170 |
|
|
|
| 171 |
|
|
Claude E. Shannon's classic 1937 thesis is described separately
|
| 172 |
|
|
in several places. From \cite{{bibref:w:boolealghist01}}:
|
| 173 |
|
|
|
| 174 |
|
|
\begin{quote}
|
| 175 |
|
|
Shannon, whose 1937 thesis centered on the improvement of the
|
| 176 |
|
|
Differential Analyzer, a clunky mechanical gear and shaft addition
|
| 177 |
|
|
machine, realized that Boolean algebraic principles governed its operation.
|
| 178 |
|
|
He proposed that such a machine could be built with circuits using
|
| 179 |
|
|
components that were governed by Boolean principles. Shannon's paper
|
| 180 |
|
|
was regarded as genius and his ideas were almost immediately
|
| 181 |
|
|
incorporated into the telephone system. Shannon took a position at Bell
|
| 182 |
|
|
Labs. Later, of course, Shannon's thesis came to be seen as a focal point
|
| 183 |
|
|
in the development of modern computers.
|
| 184 |
|
|
\end{quote}
|
| 185 |
|
|
|
| 186 |
|
|
In \cite{bibref:w:boolealghist02}, Shannon's thesis is described
|
| 187 |
|
|
very favorably:
|
| 188 |
|
|
|
| 189 |
|
|
\begin{quote}
|
| 190 |
|
|
Around the 1850's, the British mathematician George Boole was
|
| 191 |
|
|
busily inventing a new form of mathematics, in which he represented
|
| 192 |
|
|
logical expressions in a mathematical form now known as
|
| 193 |
|
|
Boolean Algebra.
|
| 194 |
|
|
|
| 195 |
|
|
Unfortunately, with the exception of students of philosophy
|
| 196 |
|
|
and symbolic logic, Boolean Algebra was destined to remain
|
| 197 |
|
|
largely unknown and unused for the better part of a century.
|
| 198 |
|
|
It fact it was not until 1938 that Claude E. Shannon published
|
| 199 |
|
|
an article based on his master's thesis at MIT. (Shannon's
|
| 200 |
|
|
thesis has since been described as: \emph{``Possibly the
|
| 201 |
|
|
most important master's thesis of the twentieth century.''})
|
| 202 |
|
|
|
| 203 |
|
|
In his paper, which was widely circulated, Shannon showed how
|
| 204 |
|
|
Boole's concepts of TRUE and FALSE could be used to represent
|
| 205 |
|
|
the functions of switches in electronic circuits. It is difficult
|
| 206 |
|
|
to convey just how important this concept was; suffice it to say
|
| 207 |
|
|
that Shannon had provided electronics engineers with the mathematical
|
| 208 |
|
|
tool they needed to design digital electronic circuits, and these
|
| 209 |
|
|
techniques remain the cornerstone of digital electronic
|
| 210 |
|
|
design to this day.
|
| 211 |
|
|
|
| 212 |
|
|
Apropos of nothing at all, Shannon is also credited with the invention
|
| 213 |
|
|
of the rocket-powered Frisbee, and is famous for riding down the
|
| 214 |
|
|
corridors of Bell Laboratories on a unicycle while simultaneously
|
| 215 |
|
|
juggling four balls.
|
| 216 |
|
|
\end{quote}
|
| 217 |
|
|
|
| 218 |
|
|
In summary, in 1854 George Boole published his classic work
|
| 219 |
|
|
\emph{An investigation into the Laws of Thought, on
|
| 220 |
|
|
Which are founded the Mathematical Theories of Logic and Probabilities},
|
| 221 |
|
|
which laid the foundation of manipulation of
|
| 222 |
|
|
logical ideas using algebraic mechanisms. Boole's ideas
|
| 223 |
|
|
were revived in 1937 and 1938 by Claude E. Shannon
|
| 224 |
|
|
in his master's thesis and a subsequent article, in which
|
| 225 |
|
|
Shannon applied Boole's ideas to the design of electric
|
| 226 |
|
|
switching circuits. Shannon's reapplication of Boole's work
|
| 227 |
|
|
came to be seen as a focal point in the development of modern
|
| 228 |
|
|
computers.
|
| 229 |
|
|
|
| 230 |
|
|
|
| 231 |
|
|
\section[Simplification By Algebraic Manipulation]
|
| 232 |
|
|
{Simplification Of Boolean Functions By Algebraic Manipulation}
|
| 233 |
|
|
%Section Tag: SAM0
|
| 234 |
|
|
\label{cbal0:ssam0}
|
| 235 |
|
|
|
| 236 |
|
|
We assume that the reader has had previous exposure to
|
| 237 |
|
|
\index{Boolean function!simplification of}simplification of
|
| 238 |
|
|
Boolean functions. For this reason, this section is a review (it is terse
|
| 239 |
|
|
and moves quickly). (For readers without this background, we
|
| 240 |
|
|
recommend \cite{bibref:b:manodigitaldesignseconded}.)
|
| 241 |
|
|
|
| 242 |
|
|
The most direct way to simplify Boolean functions is
|
| 243 |
|
|
\index{Boolean function!algebraic simplification}\emph{algebraic}
|
| 244 |
|
|
transformation---to use transformation postulates and
|
| 245 |
|
|
theorems to transform algebraic
|
| 246 |
|
|
expressions to a more desirable equivalent form.
|
| 247 |
|
|
|
| 248 |
|
|
|
| 249 |
|
|
\subsection{Nomenclature And Operators}
|
| 250 |
|
|
%Subsection Tag: NOM0
|
| 251 |
|
|
\label{cbal0:ssam0:snom0}
|
| 252 |
|
|
|
| 253 |
|
|
We define the set of two elements which we will use in
|
| 254 |
|
|
two-valued Boolean
|
| 255 |
|
|
algebra as `0' and '1' (or alternatively as
|
| 256 |
|
|
`FALSE' and `TRUE', respectively).
|
| 257 |
|
|
All functions which we will describe subsequently require
|
| 258 |
|
|
inputs which are members of this set and will produce outputs
|
| 259 |
|
|
which are also members of this set.
|
| 260 |
|
|
|
| 261 |
|
|
The \emph{complement} or \emph{negation} operator (or function)
|
| 262 |
|
|
maps from 0$\rightarrow$1 and from 1$\rightarrow$0 (see Table
|
| 263 |
|
|
\ref{tbl:cbal0:ssam0:snom0:01}).
|
| 264 |
|
|
We denote this operator
|
| 265 |
|
|
by an apostrophe
|
| 266 |
|
|
following the variable to be complemented (example: $x'$).
|
| 267 |
|
|
Alternatively, in some circumstances, we may use the
|
| 268 |
|
|
tilde ($\sim{}x$), the overbar ($\overline{x}$), or
|
| 269 |
|
|
the negation symbol ($\neg{}x$).
|
| 270 |
|
|
|
| 271 |
|
|
\begin{table}
|
| 272 |
|
|
\caption{Definition Of Logical Complement, Logical And, Logical Or, And Logical
|
| 273 |
|
|
Exclusive Or Operators}
|
| 274 |
|
|
\label{tbl:cbal0:ssam0:snom0:01}
|
| 275 |
|
|
\begin{center}
|
| 276 |
|
|
\begin{tabular}{|c|c||c|c|c|c|}
|
| 277 |
|
|
\hline
|
| 278 |
|
|
$X$ & $Y$ & $X'$ & $XY$ & $X+Y$ & $X \oplus{} Y$ \\
|
| 279 |
|
|
\hline
|
| 280 |
|
|
\hline
|
| 281 |
|
|
0 & 0 & 1 & 0 & 0 & 0 \\
|
| 282 |
|
|
\hline
|
| 283 |
|
|
0 & 1 & 1 & 0 & 1 & 1 \\
|
| 284 |
|
|
\hline
|
| 285 |
|
|
1 & 0 & 0 & 0 & 1 & 1 \\
|
| 286 |
|
|
\hline
|
| 287 |
|
|
1 & 1 & 0 & 1 & 1 & 0 \\
|
| 288 |
|
|
\hline
|
| 289 |
|
|
\end{tabular}
|
| 290 |
|
|
\end{center}
|
| 291 |
|
|
\end{table}
|
| 292 |
|
|
|
| 293 |
|
|
The \emph{logical AND} (or simply \index{AND}\index{Boolean algebra!AND}\emph{AND})
|
| 294 |
|
|
operator (or function)
|
| 295 |
|
|
returns TRUE if both of its input arguments are TRUE
|
| 296 |
|
|
(see Table
|
| 297 |
|
|
\ref{tbl:cbal0:ssam0:snom0:01}).
|
| 298 |
|
|
We denote this operator
|
| 299 |
|
|
by the \emph{times} symbol (example: $x \times{} y$), by
|
| 300 |
|
|
the keyword `AND', or by placing the operands adjacent to
|
| 301 |
|
|
each other (examples: $xy$, $x(y)$).
|
| 302 |
|
|
|
| 303 |
|
|
The \emph{logical OR}
|
| 304 |
|
|
(or simply \index{OR}\index{Boolean algebra!OR}\emph{OR})
|
| 305 |
|
|
operator (or function)
|
| 306 |
|
|
returns TRUE if either of its input arguments are TRUE
|
| 307 |
|
|
(see Table
|
| 308 |
|
|
\ref{tbl:cbal0:ssam0:snom0:01}).
|
| 309 |
|
|
We denote this operator
|
| 310 |
|
|
by the \emph{plus} symbol (example: $x + y$) or by
|
| 311 |
|
|
the keyword `OR'.
|
| 312 |
|
|
|
| 313 |
|
|
The \emph{logical exclusive-OR}
|
| 314 |
|
|
(or simply \index{XOR}\index{Boolean algebra!XOR} \emph{XOR})
|
| 315 |
|
|
operator (or function)
|
| 316 |
|
|
returns TRUE if either but not both of its input arguments are TRUE
|
| 317 |
|
|
(see Table
|
| 318 |
|
|
\ref{tbl:cbal0:ssam0:snom0:01}).
|
| 319 |
|
|
We denote this operator
|
| 320 |
|
|
by the \emph{circled plus} symbol (example: $x \oplus{} y$),
|
| 321 |
|
|
by the \emph{caret} character (example: $x$\^{}$y$), or by
|
| 322 |
|
|
the keyword `XOR'.
|
| 323 |
|
|
|
| 324 |
|
|
The exclusive-OR function is not a
|
| 325 |
|
|
function traditionally considered in the canonical forms of Boolean
|
| 326 |
|
|
algebra. However, we consider it here because our aims may in
|
| 327 |
|
|
some cases be subtly
|
| 328 |
|
|
different than the aims of classic two-valued Boolean algebra.
|
| 329 |
|
|
The goal of classic Boolean algebra is to minimize the number of
|
| 330 |
|
|
terms which appear in a canonical form.
|
| 331 |
|
|
However, often our goal here is to rearrange Boolean functions into a form
|
| 332 |
|
|
which is optimal for implementation on a computer. Since actual
|
| 333 |
|
|
computers usually provide a bitwise exclusive-OR instruction, there
|
| 334 |
|
|
are some applications where it may be useful to consider the
|
| 335 |
|
|
underlying instruction set of the computer (for example,
|
| 336 |
|
|
see \emph{Vertical Counters},
|
| 337 |
|
|
Section \ref{cbal0:svct0}).
|
| 338 |
|
|
|
| 339 |
|
|
In general, there are $2^{2^N}$ different Boolean functions of $N$
|
| 340 |
|
|
input variables, so it isn't practical to name functions involving more
|
| 341 |
|
|
than 2 input variables. There are 16 ($=2^{2^2}$) Boolean functions of
|
| 342 |
|
|
2 input variables, and these are enumerated in
|
| 343 |
|
|
Table \ref{tbl:cbal0:ssam0:snom0:02}.
|
| 344 |
|
|
|
| 345 |
|
|
\begin{table}
|
| 346 |
|
|
\caption{Sixteen Possible Boolean Functions $f(A,B)$ Of Two Boolean Variables}
|
| 347 |
|
|
\label{tbl:cbal0:ssam0:snom0:02}
|
| 348 |
|
|
\begin{center}
|
| 349 |
|
|
\begin{tabular}{|c||c|c|c|c||l|}
|
| 350 |
|
|
\hline
|
| 351 |
|
|
\small{Func.} & $\scriptstyle{f(1,1)}$ & $\scriptstyle{f(1,0)}$
|
| 352 |
|
|
& $\scriptstyle{f(0,1)}$ & $\scriptstyle{f(0,0)}$
|
| 353 |
|
|
& Function Description \\
|
| 354 |
|
|
\small{Num.} & & & & & \\
|
| 355 |
|
|
\hline
|
| 356 |
|
|
\hline
|
| 357 |
|
|
0 & 0 & 0 & 0 & 0 & \small{``Zero'' or ``clear'' function. Always} \\
|
| 358 |
|
|
& & & & & \small{returns zero regardless of $A$ and $B$ } \\
|
| 359 |
|
|
& & & & & \small{input values. } \\
|
| 360 |
|
|
\hline
|
| 361 |
|
|
1 & 0 & 0 & 0 & 1 & \small{Logical NOR = $(A+B)'$. } \\
|
| 362 |
|
|
\hline
|
| 363 |
|
|
2 & 0 & 0 & 1 & 0 & \small{Inhibition = $BA'$. So named because } \\
|
| 364 |
|
|
& & & & & \small{a TRUE value of $A$ inhibits $B$. Also } \\
|
| 365 |
|
|
& & & & & \small{equivalent to $B>A$ or to $A<B$. } \\
|
| 366 |
|
|
\hline
|
| 367 |
|
|
3 & 0 & 0 & 1 & 1 & \small{NOT A = $A'$. Ignores $B$ and returns } \\
|
| 368 |
|
|
& & & & & \small{$A'$. } \\
|
| 369 |
|
|
\hline
|
| 370 |
|
|
4 & 0 & 1 & 0 & 0 & \small{Inhibition = $AB'$. So named because } \\
|
| 371 |
|
|
& & & & & \small{a TRUE value of $B$ inhibits $A$. Also } \\
|
| 372 |
|
|
& & & & & \small{equivalent to $A>B$ or to $B<A$. } \\
|
| 373 |
|
|
\hline
|
| 374 |
|
|
5 & 0 & 1 & 0 & 1 & \small{NOT B = $B'$. Ignores $A$ and returns } \\
|
| 375 |
|
|
& & & & & \small{$B'$. } \\
|
| 376 |
|
|
\hline
|
| 377 |
|
|
6 & 0 & 1 & 1 & 0 & \small{Exclusive-OR (XOR) = $A \oplus B$. Also} \\
|
| 378 |
|
|
& & & & & \small{equivalent to $A \neq B$. } \\
|
| 379 |
|
|
\hline
|
| 380 |
|
|
7 & 0 & 1 & 1 & 1 & \small{Logical NAND = $(AB)'$. } \\
|
| 381 |
|
|
\hline
|
| 382 |
|
|
8 & 1 & 0 & 0 & 0 & \small{Logical AND = $AB$. } \\
|
| 383 |
|
|
\hline
|
| 384 |
|
|
9 & 1 & 0 & 0 & 1 & \small{Equivalence: true if $A=B$. Also} \\
|
| 385 |
|
|
& & & & & \small{known as exclusive-NOR, i.e. $(A \oplus B)'$.} \\
|
| 386 |
|
|
\hline
|
| 387 |
|
|
10 & 1 & 0 & 1 & 0 & \small{Copy $B$. Ignores $A$ and returns $B$. } \\
|
| 388 |
|
|
\hline
|
| 389 |
|
|
11 & 1 & 0 & 1 & 1 & \small{Implication: $B \rightarrow A$ (if $B$ } \\
|
| 390 |
|
|
& & & & & \small{then $A$). Also equivalent to $B \geq A$.} \\
|
| 391 |
|
|
\hline
|
| 392 |
|
|
12 & 1 & 1 & 0 & 0 & \small{Copy $A$. Ignores $B$ and returns $A$. } \\
|
| 393 |
|
|
\hline
|
| 394 |
|
|
13 & 1 & 1 & 0 & 1 & \small{Implication: $A \rightarrow B$ (if $A$ } \\
|
| 395 |
|
|
& & & & & \small{then $B$). Also equivalent to $A \geq B$.} \\
|
| 396 |
|
|
\hline
|
| 397 |
|
|
14 & 1 & 1 & 1 & 0 & \small{Logical OR = $A+B$. } \\
|
| 398 |
|
|
\hline
|
| 399 |
|
|
15 & 1 & 1 & 1 & 1 & \small{``One'' or ``set'' function. Always } \\
|
| 400 |
|
|
& & & & & \small{returns one regardless of $A$ and $B$ } \\
|
| 401 |
|
|
& & & & & \small{input values. } \\
|
| 402 |
|
|
\hline
|
| 403 |
|
|
\end{tabular}
|
| 404 |
|
|
\end{center}
|
| 405 |
|
|
\end{table}
|
| 406 |
|
|
|
| 407 |
|
|
\emph{Any} Boolean function can be synthesized using AND gates and inverters
|
| 408 |
|
|
(i.e. NOT gates), OR gates and inverters, NAND gates alone, or NOR
|
| 409 |
|
|
gates alone. However, not all Boolean functions can be synthesized
|
| 410 |
|
|
using AND gates alone or OR gates alone.
|
| 411 |
|
|
|
| 412 |
|
|
|
| 413 |
|
|
\subsection{Postulates And Theorems}
|
| 414 |
|
|
%Subsection Tag: POS0
|
| 415 |
|
|
\label{cbal0:ssam0:spos0}
|
| 416 |
|
|
|
| 417 |
|
|
Mathematicians tend to be very picky about what exactly a
|
| 418 |
|
|
\emph{postulate} is versus what a \emph{theorem} is. We are
|
| 419 |
|
|
far less picky. Either one (a postulate or a theorem) is a
|
| 420 |
|
|
rule that can be used to transform a Boolean algebraic expression
|
| 421 |
|
|
into another expression which is equivalent but for one reason or another
|
| 422 |
|
|
more desirable. For our purposes here, postulates and theorems
|
| 423 |
|
|
are interchangeable.
|
| 424 |
|
|
|
| 425 |
|
|
Table \ref{tbl:cbal0:ssam0:spos0:01}
|
| 426 |
|
|
(from \cite{bibref:b:manodigitaldesignseconded})
|
| 427 |
|
|
supplies the important postulates and theorems which are useful in
|
| 428 |
|
|
algebraically simplifying Boolean functions.
|
| 429 |
|
|
|
| 430 |
|
|
In Table \ref{tbl:cbal0:ssam0:spos0:01}, we should explain what
|
| 431 |
|
|
is meant by the \emph{Dual Postulate Or Theorem}. To
|
| 432 |
|
|
quote \cite{bibref:b:manodigitaldesignseconded}, p. 41:
|
| 433 |
|
|
|
| 434 |
|
|
\begin{quote}
|
| 435 |
|
|
\ldots This important property of Boolean algebra is called
|
| 436 |
|
|
the \index{Boolean algebra!duality principle}\index{duality principle}%
|
| 437 |
|
|
\emph{duality principle}.
|
| 438 |
|
|
It states that every algebraic expression deducible from the postulates
|
| 439 |
|
|
of Boolean algebra remains valid if the operators and identity
|
| 440 |
|
|
elements are interchanged. In a two-valued Boolean algebra,
|
| 441 |
|
|
the identity elements and the elements of the set $B$ are the
|
| 442 |
|
|
same: 1 and 0. The duality principle has many applications.
|
| 443 |
|
|
If the \emph{dual} of an algebraic expression is desired, we
|
| 444 |
|
|
simply interchange OR and AND operators and replaces 1s by
|
| 445 |
|
|
0s and 0s by 1s.
|
| 446 |
|
|
\end{quote}
|
| 447 |
|
|
|
| 448 |
|
|
\begin{table}
|
| 449 |
|
|
\caption{Important Postulates And Theorems Of Two-Valued Boolean Algebra}
|
| 450 |
|
|
\label{tbl:cbal0:ssam0:spos0:01}
|
| 451 |
|
|
\begin{center}
|
| 452 |
|
|
\begin{tabular}{|c||c|c||l|}
|
| 453 |
|
|
\hline
|
| 454 |
|
|
\small{Postulate} & \small{Postulate} & \small{Dual} & \small{Remarks} \\
|
| 455 |
|
|
\small{Or} & \small{Or} & \small{Postulate} & \\
|
| 456 |
|
|
\small{Theorem} & \small{Theorem} & \small{Or} & \\
|
| 457 |
|
|
\small{Number} & & \small{Theorem} & \\
|
| 458 |
|
|
\hline
|
| 459 |
|
|
1 & $x + 0 = x$ & $x \cdot 1 = 1$ & \\
|
| 460 |
|
|
\hline
|
| 461 |
|
|
2 & $x + x' = 1$ & $x \cdot x' = 0$ & \\
|
| 462 |
|
|
\hline
|
| 463 |
|
|
3 & $x + x = x$ & $x \cdot x = x$ & \\
|
| 464 |
|
|
\hline
|
| 465 |
|
|
4 & $x + 1 = 1$ & $x \cdot 0 = 0$ & \\
|
| 466 |
|
|
\hline
|
| 467 |
|
|
5 & $(x')' = x$ & & \small{Involution.} \\
|
| 468 |
|
|
\hline
|
| 469 |
|
|
6 & $x + y = y + x$ & $x \cdot y = y \cdot x $ & \small{Commutative property.} \\
|
| 470 |
|
|
\hline
|
| 471 |
|
|
7 & $x + (y + z)$ & $x(yz) = (xy)z$ & \small{Associative property.} \\
|
| 472 |
|
|
& $= (x + y) + z$ & & \\
|
| 473 |
|
|
\hline
|
| 474 |
|
|
8 & $x (y + z)$ & $x + yz$ & \small{Distributive property.} \\
|
| 475 |
|
|
& $= xy + xz$ & $= (x+y)(x+z)$ & \\
|
| 476 |
|
|
\hline
|
| 477 |
|
|
9 & $(x+y)' = x'y'$ & $(xy)' = x' + y'$ & \small{DeMorgan's theorem.} \\
|
| 478 |
|
|
\hline
|
| 479 |
|
|
10 & $x + xy = x$ & $x(x+y) = x$ & \small{Absorption.} \\
|
| 480 |
|
|
\hline
|
| 481 |
|
|
\end{tabular}
|
| 482 |
|
|
\end{center}
|
| 483 |
|
|
\end{table}
|
| 484 |
|
|
|
| 485 |
|
|
Note also from Item 8 of
|
| 486 |
|
|
Table \ref{tbl:cbal0:ssam0:spos0:01} that in Boolean algebra
|
| 487 |
|
|
AND distributes over OR and OR distributes over AND (waiting on
|
| 488 |
|
|
newsgroup posters to clarify). This is unlike ``normal'' algebra, where
|
| 489 |
|
|
in general,
|
| 490 |
|
|
|
| 491 |
|
|
\begin{equation}
|
| 492 |
|
|
x + yz \neq (x+y) (x+z).
|
| 493 |
|
|
\end{equation}
|
| 494 |
|
|
|
| 495 |
|
|
The \index{Boolean algebra!operator precedence}%
|
| 496 |
|
|
\index{operator precedence!Boolean algebra}\index{operator precedence}%
|
| 497 |
|
|
operator precedence for evaluating Boolean expressions assumed throughout
|
| 498 |
|
|
this work is:
|
| 499 |
|
|
|
| 500 |
|
|
\begin{quote}
|
| 501 |
|
|
\begin{enumerate}
|
| 502 |
|
|
\item Parenthesis.
|
| 503 |
|
|
\item NOT.
|
| 504 |
|
|
\item AND.
|
| 505 |
|
|
\item OR.
|
| 506 |
|
|
\end{enumerate}
|
| 507 |
|
|
\end{quote}
|
| 508 |
|
|
|
| 509 |
|
|
\noindent{}Note that this operator precedence very closely mirrors
|
| 510 |
|
|
the standard precedence of normal algebraic expressions.
|
| 511 |
|
|
|
| 512 |
|
|
\subsection{Canonical And Standard Forms}
|
| 513 |
|
|
%Subsection Tag: CAS0
|
| 514 |
|
|
\label{cbal0:ssam0:scas0}
|
| 515 |
|
|
|
| 516 |
|
|
\cite{bibref:b:manodigitaldesignseconded}, p. 49 provides an concise and
|
| 517 |
|
|
excellent definition of \emph{minterms} and \emph{maxterms}. The definition
|
| 518 |
|
|
here is taken primarily from that source.
|
| 519 |
|
|
|
| 520 |
|
|
A binary variable may appear either in its normal form ($x$, for example)
|
| 521 |
|
|
or in its complemented form ($x'$, for example). Now consider two
|
| 522 |
|
|
binary variables $x$ and $y$ combined with an AND
|
| 523 |
|
|
operation. Since each variable may appear in either form, there are four
|
| 524 |
|
|
possible combinations: $x'y'$, $x'y$, $xy'$, and $xy$. These
|
| 525 |
|
|
four AND terms are mutually exclusive and mutually exhaustive---that is,
|
| 526 |
|
|
no combination of values for
|
| 527 |
|
|
$x$ and
|
| 528 |
|
|
$y$ that causes one of these AND terms to be TRUE may cause any of the
|
| 529 |
|
|
others to be TRUE, and every combination of $x$ and $y$ will cause exactly
|
| 530 |
|
|
one of these AND terms to be TRUE. Each of these
|
| 531 |
|
|
four AND terms is called a \index{Boolean algebra!minterm}\index{minterm}\emph{minterm}
|
| 532 |
|
|
or \index{Boolean algebra!standard product}\index{standard product}\emph{standard product}.
|
| 533 |
|
|
In a similar manner, $n$ variables can be combined to form $2^n$ minterms.
|
| 534 |
|
|
|
| 535 |
|
|
In a similar fashion, $n$ variables forming an OR term, with each variable
|
| 536 |
|
|
being primed or unprimed, provide $2^n$ possible combinations, called
|
| 537 |
|
|
\index{Boolean algebra!maxterm}\index{maxterm}\emph{maxterms}, or
|
| 538 |
|
|
\index{Boolean algebra!standard sum}\index{standard sum}\emph{standard sums}.
|
| 539 |
|
|
|
| 540 |
|
|
\begin{table}
|
| 541 |
|
|
\caption{Minterms And Maxterms Of Three Boolean Variables}
|
| 542 |
|
|
\label{tbl:cbal0:ssam0:scas0:01}
|
| 543 |
|
|
\begin{center}
|
| 544 |
|
|
\begin{tabular}{|c|c|c||c|c||c|c|}
|
| 545 |
|
|
\hline
|
| 546 |
|
|
$x$ & $y$ & $z$ & \small{Minterm} & \small{Minterm} & \small{Maxterm} & \small{Maxterm} \\
|
| 547 |
|
|
& & & \small{Term} & \small{Designation} & \small{Term} & \small{Designation} \\
|
| 548 |
|
|
\hline
|
| 549 |
|
|
0 & 0 & 0 & $x'y'z'$ & $m_0$ & $x+y+z$ & $M_0$ \\
|
| 550 |
|
|
\hline
|
| 551 |
|
|
0 & 0 & 1 & $x'y'z$ & $m_1$ & $x+y+z'$ & $M_1$ \\
|
| 552 |
|
|
\hline
|
| 553 |
|
|
0 & 1 & 0 & $x'yz'$ & $m_2$ & $x+y'+z$ & $M_2$ \\
|
| 554 |
|
|
\hline
|
| 555 |
|
|
0 & 1 & 1 & $x'yz$ & $m_3$ & $x+y'+z'$ & $M_3$ \\
|
| 556 |
|
|
\hline
|
| 557 |
|
|
1 & 0 & 0 & $xy'z'$ & $m_4$ & $x'+y+z$ & $M_4$ \\
|
| 558 |
|
|
\hline
|
| 559 |
|
|
0 & 0 & 1 & $x'y'z$ & $m_5$ & $x+y+z'$ & $M_5$ \\
|
| 560 |
|
|
\hline
|
| 561 |
|
|
1 & 1 & 0 & $xyz'$ & $m_6$ & $x'+y'+z$ & $M_6$ \\
|
| 562 |
|
|
\hline
|
| 563 |
|
|
1 & 1 & 1 & $xyz$ & $m_7$ & $x'+y'+z'$ & $M_7$ \\
|
| 564 |
|
|
\hline
|
| 565 |
|
|
\end{tabular}
|
| 566 |
|
|
\end{center}
|
| 567 |
|
|
\end{table}
|
| 568 |
|
|
|
| 569 |
|
|
The two primary canonical forms in Boolean algebra are the
|
| 570 |
|
|
\emph{sum of minterms} (or \emph{sum of products}) form and the
|
| 571 |
|
|
\emph{product of maxterms} (or \emph{product of sums}) form.
|
| 572 |
|
|
|
| 573 |
|
|
The sum of minterms canonical form (which is the most common
|
| 574 |
|
|
canonical form) is sometimes written using a shorthand
|
| 575 |
|
|
notation involving the Greek letter sigma ($\Sigma$). We describe this
|
| 576 |
|
|
shorthand form now. Consider the Boolean function of 3 variables,
|
| 577 |
|
|
|
| 578 |
|
|
\begin{equation}
|
| 579 |
|
|
\label{eq:cbal0:ssam0:scas0:01}
|
| 580 |
|
|
F(A, B, C) = A + B'C.
|
| 581 |
|
|
\end{equation}
|
| 582 |
|
|
|
| 583 |
|
|
\noindent{}Using the postulates and theorems in Table
|
| 584 |
|
|
\ref{tbl:cbal0:ssam0:spos0:01}, it is possible
|
| 585 |
|
|
to expand (\ref{eq:cbal0:ssam0:scas0:01}) into
|
| 586 |
|
|
a sum of minterms form:
|
| 587 |
|
|
|
| 588 |
|
|
\begin{eqnarray}
|
| 589 |
|
|
\label{eq:cbal0:ssam0:scas0:02}
|
| 590 |
|
|
F(A, B, C) & = & A'B'C + AB'C' + AB'C + ABC' + ABC \\
|
| 591 |
|
|
& = & m_1 m_4 m_5 m_6 m_7.\nonumber
|
| 592 |
|
|
\end{eqnarray}
|
| 593 |
|
|
|
| 594 |
|
|
\noindent{}(\ref{eq:cbal0:ssam0:scas0:02}) is also commonly written
|
| 595 |
|
|
in the shorthand form:
|
| 596 |
|
|
|
| 597 |
|
|
\begin{equation}
|
| 598 |
|
|
\label{eq:cbal0:ssam0:scas0:03}
|
| 599 |
|
|
F(A, B, C) = \Sigma{}(1, 4, 5, 6, 7).
|
| 600 |
|
|
\end{equation}
|
| 601 |
|
|
|
| 602 |
|
|
\noindent{}In the right-hand side of
|
| 603 |
|
|
(\ref{eq:cbal0:ssam0:scas0:03}), each integer
|
| 604 |
|
|
(1, 4, 5, 6, or 7) corresponds to the integer
|
| 605 |
|
|
that would be formed by treating the corresponding
|
| 606 |
|
|
minterm in (\ref{eq:cbal0:ssam0:scas0:02}) as
|
| 607 |
|
|
a binary number, i.e. $A=2^2$, $B=2^1$, and
|
| 608 |
|
|
$C=2^0$. This is the basis of the short hand
|
| 609 |
|
|
notation.
|
| 610 |
|
|
|
| 611 |
|
|
A second but much less commonly used canonical form
|
| 612 |
|
|
is the product of maxterms (or product of sums) form,
|
| 613 |
|
|
which uses the Greek letter pi ($\Pi$) for its shorthand
|
| 614 |
|
|
form. Without further explanation, we present the
|
| 615 |
|
|
product of maxterms form of $\Sigma{}(1,4,5,6,7)$
|
| 616 |
|
|
(Eqns. \ref{eq:cbal0:ssam0:scas0:01} through
|
| 617 |
|
|
\ref{eq:cbal0:ssam0:scas0:03}) as
|
| 618 |
|
|
(\ref{eq:cbal0:ssam0:scas0:04})
|
| 619 |
|
|
through (\ref{eq:cbal0:ssam0:scas0:07})
|
| 620 |
|
|
(Figure \ref{fig:cbal0:ssam0:scas0:01}).
|
| 621 |
|
|
|
| 622 |
|
|
\begin{figure}
|
| 623 |
|
|
\begin{eqnarray}
|
| 624 |
|
|
\label{eq:cbal0:ssam0:scas0:04}
|
| 625 |
|
|
F(A, B, C) & = & \Sigma{}(1, 4, 5, 6, 7) \\
|
| 626 |
|
|
\label{eq:cbal0:ssam0:scas0:05}
|
| 627 |
|
|
& = & \Pi{}(0, 2, 3) \\
|
| 628 |
|
|
\label{eq:cbal0:ssam0:scas0:06}
|
| 629 |
|
|
& = & M_0 M_2 M_3 \\
|
| 630 |
|
|
\label{eq:cbal0:ssam0:scas0:07}
|
| 631 |
|
|
& = & (x+y+z)(x+y'+z)(x+y'+z')
|
| 632 |
|
|
\end{eqnarray}
|
| 633 |
|
|
\caption{Product Of Maxterms Form Of $\Sigma{}(1,4,5,6,7)$}
|
| 634 |
|
|
\label{fig:cbal0:ssam0:scas0:01}
|
| 635 |
|
|
\end{figure}
|
| 636 |
|
|
|
| 637 |
|
|
|
| 638 |
|
|
Because there are so many excellent digital logic books on the market
|
| 639 |
|
|
that contain examples and exercises of algebraic simplification
|
| 640 |
|
|
(we recommend \cite{bibref:b:manodigitaldesignseconded}), we don't
|
| 641 |
|
|
dwell on algebraic simplification or provide examples. Again, we
|
| 642 |
|
|
assume that nearly all of our readers have had a course in digital
|
| 643 |
|
|
logic or symbolic logic.
|
| 644 |
|
|
|
| 645 |
|
|
|
| 646 |
|
|
\section[Karnaugh Maps]
|
| 647 |
|
|
{Simplification Of Boolean Functions Using Karnaugh Maps}
|
| 648 |
|
|
%Section tag: SKM0
|
| 649 |
|
|
\label{cbal0:skm0}
|
| 650 |
|
|
|
| 651 |
|
|
In 1953, M. Karnaugh published the graphical map method of simplifying
|
| 652 |
|
|
combinational logic functions (\cite{bibref:p:kmapclassic01}). This
|
| 653 |
|
|
method has come to be known as the \emph{Karnaugh map} or \emph{K-map}
|
| 654 |
|
|
method of reduction, and is taught to engineers in nearly every
|
| 655 |
|
|
digital logic class.
|
| 656 |
|
|
|
| 657 |
|
|
Although it is possible, starting from an arbitrary Boolean formula, to simplify
|
| 658 |
|
|
the formula through algebraic manipulation, algebraic simplification
|
| 659 |
|
|
has the disadvantage that formulas can have many forms and there is not
|
| 660 |
|
|
an easily remembered, precise, and repeatable procedure for algebraic simplification.
|
| 661 |
|
|
The Karnaugh map method has the advantage that each Boolean function
|
| 662 |
|
|
has only one graphical representation, and that the procedure for simplification
|
| 663 |
|
|
is simple and easily remembered.
|
| 664 |
|
|
|
| 665 |
|
|
In a Karnaugh map, each square corresponds to a possible minterm of the function.
|
| 666 |
|
|
The essence of the method is to populate a grid of squares with outputs of
|
| 667 |
|
|
the function to be simplified. Each minterm that must exist in the
|
| 668 |
|
|
function (i.e. each combination of inputs for which the function
|
| 669 |
|
|
must return TRUE) receives a `1' in the corresponding square. Each
|
| 670 |
|
|
combination of inputs for which the function must return FALSE
|
| 671 |
|
|
receives a `0' in the corresponding square. Each combination of inputs
|
| 672 |
|
|
for which the function may return either TRUE or FALSE receives an
|
| 673 |
|
|
`X' in the corresponding square.
|
| 674 |
|
|
|
| 675 |
|
|
After the Karnaugh map squares are populated with 1's, 0's, and X's
|
| 676 |
|
|
corresponding to the required values of the function for each combination
|
| 677 |
|
|
of inputs, the 1's are graphically combined into the largest rectangle possible.
|
| 678 |
|
|
Each rectangle may include 1's, may include X's where convenient, but
|
| 679 |
|
|
may not include 0's.
|
| 680 |
|
|
Each of these squares is then translated into a product of uncomplemented and
|
| 681 |
|
|
complemented input variables, and these products are summed to
|
| 682 |
|
|
produce the simplified algebraic expression for the function. (We don't
|
| 683 |
|
|
belabor this process, because we assume that most of our readers
|
| 684 |
|
|
understand it very thoroughly.) There are some subtle points
|
| 685 |
|
|
to the process, such as combining corners and the ``folding'' of the
|
| 686 |
|
|
5- and 6-variable maps, but we don't explain these subtle points here
|
| 687 |
|
|
because they are so thoroughly explained in so many books.
|
| 688 |
|
|
|
| 689 |
|
|
Figures \ref{fig:cbal0:skm0:00} through \ref{fig:cbal0:skm0:04}
|
| 690 |
|
|
supply the canonical forms of two-, three-, four-, five-, and
|
| 691 |
|
|
six-variable Karnaugh maps.
|
| 692 |
|
|
|
| 693 |
|
|
\begin{figure}
|
| 694 |
|
|
\centering
|
| 695 |
|
|
\includegraphics[width=1.25in]{c_bal0/kmap02cf.eps}
|
| 696 |
|
|
\caption{Canonical Form Of Two-Variable Karnaugh Map}
|
| 697 |
|
|
\label{fig:cbal0:skm0:00}
|
| 698 |
|
|
\end{figure}
|
| 699 |
|
|
|
| 700 |
|
|
\begin{figure}
|
| 701 |
|
|
\centering
|
| 702 |
|
|
\includegraphics[height=1.25in]{c_bal0/kmap03cf.eps}
|
| 703 |
|
|
\caption{Canonical Form Of Three-Variable Karnaugh Map}
|
| 704 |
|
|
\label{fig:cbal0:skm0:01}
|
| 705 |
|
|
\end{figure}
|
| 706 |
|
|
|
| 707 |
|
|
\begin{figure}
|
| 708 |
|
|
\centering
|
| 709 |
|
|
\includegraphics[height=2.0in]{c_bal0/kmap04cf.eps}
|
| 710 |
|
|
\caption{Canonical Form Of Four-Variable Karnaugh Map}
|
| 711 |
|
|
\label{fig:cbal0:skm0:02}
|
| 712 |
|
|
\end{figure}
|
| 713 |
|
|
|
| 714 |
|
|
\begin{figure}
|
| 715 |
|
|
\centering
|
| 716 |
|
|
\includegraphics[width=4.25in]{c_bal0/kmap05cf.eps}
|
| 717 |
|
|
\caption{Canonical Form Of Five-Variable Karnaugh Map}
|
| 718 |
|
|
\label{fig:cbal0:skm0:03}
|
| 719 |
|
|
\end{figure}
|
| 720 |
|
|
|
| 721 |
|
|
\begin{figure}
|
| 722 |
|
|
\centering
|
| 723 |
|
|
\includegraphics[width=4.5in]{c_bal0/kmap06cf.eps}
|
| 724 |
|
|
\caption{Canonical Form Of Six-Variable Karnaugh Map}
|
| 725 |
|
|
\label{fig:cbal0:skm0:04}
|
| 726 |
|
|
\end{figure}
|
| 727 |
|
|
|
| 728 |
|
|
\section[Simplification Using The Scheinman Method]
|
| 729 |
|
|
{Simplification Of Boolean Functions Using The Scheinman Method}
|
| 730 |
|
|
%Section Tag: SCM0
|
| 731 |
|
|
\label{cbal0:sscm0}
|
| 732 |
|
|
|
| 733 |
|
|
Two major disadvantages of the Karnaugh map method of simplifying Boolean
|
| 734 |
|
|
functions are that:
|
| 735 |
|
|
|
| 736 |
|
|
\begin{itemize}
|
| 737 |
|
|
\item It is generally not possible to apply the method to functions
|
| 738 |
|
|
of more than six variables.
|
| 739 |
|
|
\item It is not easy to automate the method (in the form that it is stated)
|
| 740 |
|
|
because it is inherently graphical.
|
| 741 |
|
|
\end{itemize}
|
| 742 |
|
|
|
| 743 |
|
|
In 1962, A. H. Scheinman published a method for the simplification
|
| 744 |
|
|
of Boolean functions (\cite{bibref:p:scheinmanclassic01}) which is more amenable
|
| 745 |
|
|
to automation than the Karnaugh map method.
|
| 746 |
|
|
|
| 747 |
|
|
\section[The Quine-McCluskey Method]
|
| 748 |
|
|
{Simplification Of Boolean Functions Using The Quine-McCluskey Method}
|
| 749 |
|
|
|
| 750 |
|
|
|
| 751 |
|
|
\section{Multiple Functions Of $N$ Boolean Variables}
|
| 752 |
|
|
|
| 753 |
|
|
Need to get back to Dr. Singh to inquire about the multiple Scheinman method.
|
| 754 |
|
|
|
| 755 |
|
|
\section{Vertical Counters}
|
| 756 |
|
|
%Section Tag: VCT0.
|
| 757 |
|
|
\label{cbal0:svct0}
|
| 758 |
|
|
|
| 759 |
|
|
\index{vertical counter}As has been hinted at elsewhere
|
| 760 |
|
|
in this work, the need to generate
|
| 761 |
|
|
firmware which minimizes ROM consumption leads to clever (but perhaps
|
| 762 |
|
|
less-than-intuitive) programming techniques. One such technique
|
| 763 |
|
|
is the construction of \emph{vertical counters}.
|
| 764 |
|
|
|
| 765 |
|
|
A \index{vertical counter}vertical counter
|
| 766 |
|
|
is a set of identical combinational mappings or state machines
|
| 767 |
|
|
where the inputs, state vector, intermediate results, and outputs of each
|
| 768 |
|
|
combinational mapping or state machine are stored as a single bit
|
| 769 |
|
|
in the same position
|
| 770 |
|
|
in each of multiple bytes or words. When inputs, state vectors,
|
| 771 |
|
|
intermediate results, and outputs are stored
|
| 772 |
|
|
in this way, the bitwise logical instructions of the machine
|
| 773 |
|
|
(AND, OR, NOT, XOR) can be used to process several state machines in
|
| 774 |
|
|
parallel. Vertical counters are intimately related to the reduction
|
| 775 |
|
|
of Boolean functions because such reduction must be performed in order
|
| 776 |
|
|
to design the vertical counter. Debouncing and filtering, where the
|
| 777 |
|
|
inputs and outputs naturally tend to be arranged as groups of bits,
|
| 778 |
|
|
are the most common application of vertical counters.
|
| 779 |
|
|
|
| 780 |
|
|
A very helpful resource on the web is the set of web pages
|
| 781 |
|
|
maintained by \index{Dattalo, Scott}Scott Dattalo
|
| 782 |
|
|
\cite{bibref:i:scottdattalo} for the
|
| 783 |
|
|
PIC microcontroller, including
|
| 784 |
|
|
especially \cite{bibref:w:sdattalovc02}. Many of the vertical counter
|
| 785 |
|
|
designs which follow come from Mr. Dattalo's pages.
|
| 786 |
|
|
|
| 787 |
|
|
We abuse the term \emph{counter} somewhat, and we refer to
|
| 788 |
|
|
any bit-wise mapping useful in microcontroller work as
|
| 789 |
|
|
a vertical counter. We categorize vertical counters as
|
| 790 |
|
|
\index{vertical counter!combinational}\emph{combinational}
|
| 791 |
|
|
(not truly a counter---the output is a function of the
|
| 792 |
|
|
inputs only), \index{vertical counter!sequential}\emph{sequential}
|
| 793 |
|
|
(the next state and output may be functions of both the
|
| 794 |
|
|
inputs and the present state---i.e. a proper state machine),
|
| 795 |
|
|
\index{vertical counter!cyclic}\emph{cyclic} (the counter
|
| 796 |
|
|
goes through a series of states and then repeats), or
|
| 797 |
|
|
\index{vertical counter!terminating} (the counter
|
| 798 |
|
|
will reach a terminal state).
|
| 799 |
|
|
|
| 800 |
|
|
\subsection{2-Bit 4-State Cyclic Vertical Counter}
|
| 801 |
|
|
%Subsection Tag: TBF0
|
| 802 |
|
|
\label{cbal0:svct0:stbf0}
|
| 803 |
|
|
In this discussion of vertical counters, we begin with the simplest
|
| 804 |
|
|
designs, as often the simpler designs appear as part of more complex
|
| 805 |
|
|
designs.
|
| 806 |
|
|
|
| 807 |
|
|
Table \ref{tbl:cbal0:svct0:stbf0:01} supplies the state transition table
|
| 808 |
|
|
for a 2-bit 4-state
|
| 809 |
|
|
cyclic vertical counter. Note that the counter advances through the
|
| 810 |
|
|
bit patterns in the ``proper'' binary integer order.
|
| 811 |
|
|
|
| 812 |
|
|
\begin{table}
|
| 813 |
|
|
\caption{State Transition Table Of 2-Bit 4-State Cyclic Vertical Counter}
|
| 814 |
|
|
\label{tbl:cbal0:svct0:stbf0:01}
|
| 815 |
|
|
\begin{center}
|
| 816 |
|
|
\begin{tabular}{|c|c|c|c|}
|
| 817 |
|
|
\hline
|
| 818 |
|
|
$A_k$ & $B_k$ & $A_{k+1}$ & $B_{k+1}$ \\
|
| 819 |
|
|
\hline
|
| 820 |
|
|
\hline
|
| 821 |
|
|
0 & 0 & 0 & 1 \\
|
| 822 |
|
|
\hline
|
| 823 |
|
|
0 & 1 & 1 & 0 \\
|
| 824 |
|
|
\hline
|
| 825 |
|
|
1 & 0 & 1 & 1 \\
|
| 826 |
|
|
\hline
|
| 827 |
|
|
1 & 1 & 0 & 0 \\
|
| 828 |
|
|
\hline
|
| 829 |
|
|
\end{tabular}
|
| 830 |
|
|
\end{center}
|
| 831 |
|
|
\end{table}
|
| 832 |
|
|
|
| 833 |
|
|
From Table \ref{tbl:cbal0:svct0:stbf0:01} it can be readily verified
|
| 834 |
|
|
even without a Karnaugh map that the least significant bit
|
| 835 |
|
|
($B$) is always complemented from one state to the next, so that
|
| 836 |
|
|
$B_{k+1} = \neg B_k$. It can also be seen that the most significant
|
| 837 |
|
|
bit ($A$) is complemented from one state to the next only if $B$=1,
|
| 838 |
|
|
so that $A_{k+1} = A_k \oplus B_k$.
|
| 839 |
|
|
|
| 840 |
|
|
The implementation of such a counter in `C' comes immediately, since
|
| 841 |
|
|
`C' directly supports bit-wise complementation and exclusive-OR of
|
| 842 |
|
|
integers:
|
| 843 |
|
|
|
| 844 |
|
|
\begin{verbatim}
|
| 845 |
|
|
A = A ^ B;
|
| 846 |
|
|
B = ~B;
|
| 847 |
|
|
\end{verbatim}
|
| 848 |
|
|
|
| 849 |
|
|
Note in the `C' snippet above, the two operations are ordered so as
|
| 850 |
|
|
not to interfere with each other. Note that reversing the two steps above
|
| 851 |
|
|
would not yield the desired result.
|
| 852 |
|
|
|
| 853 |
|
|
|
| 854 |
|
|
\subsection{3-Bit 8-State Cyclic Vertical Counter}
|
| 855 |
|
|
%Subsection Tag: TBF4
|
| 856 |
|
|
\label{cbal0:svct0:stbf4}
|
| 857 |
|
|
|
| 858 |
|
|
|
| 859 |
|
|
\subsection[$N$-Bit $2^N$-State Cyclic Vertical Counter]
|
| 860 |
|
|
{\mbox{\boldmath $N$}-Bit \mbox{\boldmath $2^N$}-State Cyclic Vertical Counter}
|
| 861 |
|
|
%Subsection Tag: TBF1
|
| 862 |
|
|
\label{cbal0:svct0:stbf1}
|
| 863 |
|
|
|
| 864 |
|
|
The design of the 2-bit 4-state vertical counter presented in
|
| 865 |
|
|
Section \ref{cbal0:svct0:stbf0} (immediately above) and be
|
| 866 |
|
|
generalized to an $N$-bit $2^N$-state counter which follows
|
| 867 |
|
|
the traditional binary integer counting sequence.
|
| 868 |
|
|
|
| 869 |
|
|
Note from Section \ref{cbal0:svct0:stbf0} that the least
|
| 870 |
|
|
significant bit of the counter is always complemented
|
| 871 |
|
|
in going from one state to the next, and that each more
|
| 872 |
|
|
significant bit is complemented only if all less significant
|
| 873 |
|
|
bits are 1. If $X_0$ is the least significant bit of the
|
| 874 |
|
|
counter and $X_N$ the most significant bit,
|
| 875 |
|
|
(\ref{eq:cbal0:svct0:stbf1:01}) through (\ref{eq:cbal0:svct0:stbf1:05})
|
| 876 |
|
|
(Figure \ref{eq:cbal0:svct0:stbf1:01})
|
| 877 |
|
|
describe how the counter is advanced from one state to the next.
|
| 878 |
|
|
Note that this set of equations gives only a \emph{logical} description
|
| 879 |
|
|
of how to obtain the next state from the present state---these
|
| 880 |
|
|
equations cannot be used as a direct blueprint for implementation because
|
| 881 |
|
|
earlier steps would destroy the results needed for later steps.
|
| 882 |
|
|
|
| 883 |
|
|
\begin{figure}
|
| 884 |
|
|
\begin{eqnarray}
|
| 885 |
|
|
\label{eq:cbal0:svct0:stbf1:01}
|
| 886 |
|
|
X_0(k+1) & = & \neg X_0(k) \\
|
| 887 |
|
|
\label{eq:cbal0:svct0:stbf1:02}
|
| 888 |
|
|
X_1(k+1) & = & X_1(k) \oplus X_0(k) \\
|
| 889 |
|
|
\label{eq:cbal0:svct0:stbf1:03}
|
| 890 |
|
|
X_2(k+1) & = & X_2(k) \oplus (X_1(k) X_0(k)) \\
|
| 891 |
|
|
\label{eq:cbal0:svct0:stbf1:04}
|
| 892 |
|
|
X_3(k+1) & = & X_3(k) \oplus (X_2(k) X_1(k) X_0(k)) \\
|
| 893 |
|
|
& \ldots & \nonumber \\
|
| 894 |
|
|
\label{eq:cbal0:svct0:stbf1:05}
|
| 895 |
|
|
X_N(k+1) & = & X_N(k) \oplus (X_{N-1}(k) \ldots X_0(k))
|
| 896 |
|
|
\end{eqnarray}
|
| 897 |
|
|
\caption{State Transition Equations Of $N$-Bit $2^N$-State Cyclic Vertical Counter}
|
| 898 |
|
|
\label{fig:cbal0:svct0:stbf1:01}
|
| 899 |
|
|
\end{figure}
|
| 900 |
|
|
|
| 901 |
|
|
The form of
|
| 902 |
|
|
(\ref{eq:cbal0:svct0:stbf1:01}) through (\ref{eq:cbal0:svct0:stbf1:05})
|
| 903 |
|
|
suggests a way to economically implement an $N$-bit $2^N$-state
|
| 904 |
|
|
cyclic vertical counter in software, using two temporary
|
| 905 |
|
|
variables $TEMP_A$ and $TEMP_B$. The general blueprint for
|
| 906 |
|
|
implementation is supplied as
|
| 907 |
|
|
(\ref{eq:cbal0:svct0:stbf1:06}) through (\ref{eq:cbal0:svct0:stbf1:20})
|
| 908 |
|
|
(Figure \ref{eq:cbal0:svct0:stbf1:02}).
|
| 909 |
|
|
|
| 910 |
|
|
\begin{figure}
|
| 911 |
|
|
\begin{eqnarray}
|
| 912 |
|
|
\label{eq:cbal0:svct0:stbf1:06}
|
| 913 |
|
|
TEMP_A & = & X_0 \\
|
| 914 |
|
|
\label{eq:cbal0:svct0:stbf1:07}
|
| 915 |
|
|
X_0 & = & \neg X_0 \\
|
| 916 |
|
|
\label{eq:cbal0:svct0:stbf1:08}
|
| 917 |
|
|
TEMP_B & = & X_1 TEMP_A \\
|
| 918 |
|
|
\label{eq:cbal0:svct0:stbf1:09}
|
| 919 |
|
|
X_1 & = & X_1 \oplus TEMP_A \\
|
| 920 |
|
|
\label{eq:cbal0:svct0:stbf1:10}
|
| 921 |
|
|
TEMP_A & = & TEMP_B \\
|
| 922 |
|
|
\label{eq:cbal0:svct0:stbf1:11}
|
| 923 |
|
|
TEMP_B & = & X_2 TEMP_B \\
|
| 924 |
|
|
\label{eq:cbal0:svct0:stbf1:12}
|
| 925 |
|
|
X_2 & = & X_2 \oplus TEMP_A \\
|
| 926 |
|
|
\label{eq:cbal0:svct0:stbf1:13}
|
| 927 |
|
|
TEMP_A & = & TEMP_B \\
|
| 928 |
|
|
\label{eq:cbal0:svct0:stbf1:14}
|
| 929 |
|
|
TEMP_B & = & X_3 TEMP_B \\
|
| 930 |
|
|
\label{eq:cbal0:svct0:stbf1:15}
|
| 931 |
|
|
X_3 & = & X_3 \oplus TEMP_A \\
|
| 932 |
|
|
& \ldots & \nonumber \\
|
| 933 |
|
|
\label{eq:cbal0:svct0:stbf1:16}
|
| 934 |
|
|
X_{N-2} & = & X_{N-2} \oplus TEMP_A \\
|
| 935 |
|
|
\label{eq:cbal0:svct0:stbf1:17}
|
| 936 |
|
|
TEMP_A & = & TEMP_B \\
|
| 937 |
|
|
\label{eq:cbal0:svct0:stbf1:18}
|
| 938 |
|
|
TEMP_B & = & X_{N-1} TEMP_B \\
|
| 939 |
|
|
\label{eq:cbal0:svct0:stbf1:19}
|
| 940 |
|
|
X_{N-1} & = & X_{N-1} \oplus TEMP_A \\
|
| 941 |
|
|
\label{eq:cbal0:svct0:stbf1:20}
|
| 942 |
|
|
X_N & = & X_N \oplus X_N TEMP_B
|
| 943 |
|
|
\end{eqnarray}
|
| 944 |
|
|
\caption{Implementation Blueprint Of $N$-Bit $2^N$-State Cyclic Vertical Counter}
|
| 945 |
|
|
\label{fig:cbal0:svct0:stbf1:02}
|
| 946 |
|
|
\end{figure}
|
| 947 |
|
|
|
| 948 |
|
|
Figure \ref{fig:cbal0:svct0:stbf1:01}
|
| 949 |
|
|
supplies a concrete example of a C-language
|
| 950 |
|
|
implementation of a 5-bit 32-state cyclic vertical counter.
|
| 951 |
|
|
Note that the counter will follow the traditional
|
| 952 |
|
|
binary integer counting sequence. Note also that
|
| 953 |
|
|
the blueprint provided by Eqns.
|
| 954 |
|
|
(\ref{eq:cbal0:svct0:stbf1:06}) through (\ref{eq:cbal0:svct0:stbf1:20})
|
| 955 |
|
|
and Figure \ref{fig:cbal0:svct0:stbf1:01} can
|
| 956 |
|
|
be extended to a counter of any size.
|
| 957 |
|
|
|
| 958 |
|
|
\begin{figure}
|
| 959 |
|
|
\begin{verbatim}
|
| 960 |
|
|
/**************************************************************/
|
| 961 |
|
|
/* Assume: */
|
| 962 |
|
|
/* x4 : Byte containing most significant bits of the */
|
| 963 |
|
|
/* a group of 8 bits. */
|
| 964 |
|
|
/* x3, */
|
| 965 |
|
|
/* x2, */
|
| 966 |
|
|
/* x1 : Bytes containing the intermediate bits. */
|
| 967 |
|
|
/* x0 : Byte containing the least significant bits. */
|
| 968 |
|
|
/* temp_a, */
|
| 969 |
|
|
/* temp_b : Temporary variables, used to accumulate the */
|
| 970 |
|
|
/* result of AND'ing old counter bit values. */
|
| 971 |
|
|
/**************************************************************/
|
| 972 |
|
|
|
| 973 |
|
|
temp_a = x0;
|
| 974 |
|
|
x0 = ~x0;
|
| 975 |
|
|
temp_b = x1 & temp_a;
|
| 976 |
|
|
x1 = x1 ^ temp_a;
|
| 977 |
|
|
temp_a = temp_b;
|
| 978 |
|
|
temp_b = x2 & temp_b;
|
| 979 |
|
|
x2 = x2 ^ temp_a;
|
| 980 |
|
|
temp_a = temp_b;
|
| 981 |
|
|
temp_b = x3 & temp_b;
|
| 982 |
|
|
x3 = x3 ^ temp_a;
|
| 983 |
|
|
x4 = x4 ^ temp_b;
|
| 984 |
|
|
|
| 985 |
|
|
/* End of code. */
|
| 986 |
|
|
\end{verbatim}
|
| 987 |
|
|
\caption{C-Language Implementation Of 5-Bit 32-State Cyclic Vertical Counter}
|
| 988 |
|
|
\label{fig:cbal0:svct0:stbf1:01b}
|
| 989 |
|
|
\end{figure}
|
| 990 |
|
|
|
| 991 |
|
|
|
| 992 |
|
|
\subsection{3-Bit 5-State Cyclic Vertical Counter}
|
| 993 |
|
|
%Subsection Tag: TBF5
|
| 994 |
|
|
\label{cbal0:svct0:stbf5}
|
| 995 |
|
|
|
| 996 |
|
|
|
| 997 |
|
|
\subsection{3-Bit 6-State Cyclic Vertical Counter}
|
| 998 |
|
|
%Subsection Tag: TBF6
|
| 999 |
|
|
\label{cbal0:svct0:stbf6}
|
| 1000 |
|
|
|
| 1001 |
|
|
|
| 1002 |
|
|
\subsection{3-Bit 7-State Cyclic Vertical Counter}
|
| 1003 |
|
|
%Subsection Tag: TBF7
|
| 1004 |
|
|
\label{cbal0:svct0:stbf7}
|
| 1005 |
|
|
|
| 1006 |
|
|
|
| 1007 |
|
|
\subsection{2-Bit 4-State Terminating Vertical Counter}
|
| 1008 |
|
|
%Subsection Tag: TBF8
|
| 1009 |
|
|
\label{cbal0:svct0:stbf8}
|
| 1010 |
|
|
|
| 1011 |
|
|
|
| 1012 |
|
|
\subsection{3-Bit 5-State Terminating Vertical Counter}
|
| 1013 |
|
|
%Subsection Tag: TBF9
|
| 1014 |
|
|
\label{cbal0:svct0:stbf9}
|
| 1015 |
|
|
|
| 1016 |
|
|
|
| 1017 |
|
|
\subsection{3-Bit 6-State Terminating Vertical Counter}
|
| 1018 |
|
|
%Subsection Tag: TBG0
|
| 1019 |
|
|
\label{cbal0:svct0:stbg0}
|
| 1020 |
|
|
|
| 1021 |
|
|
|
| 1022 |
|
|
\subsection{3-Bit 7-State Terminating Vertical Counter}
|
| 1023 |
|
|
%Subsection Tag: TBG1
|
| 1024 |
|
|
\label{cbal0:svct0:stbg1}
|
| 1025 |
|
|
|
| 1026 |
|
|
|
| 1027 |
|
|
\subsection{2/3 Debouncing Vertical Counter}
|
| 1028 |
|
|
%Subsection Tag: TTD0.
|
| 1029 |
|
|
\label{cbal0:svct0:sttd0}
|
| 1030 |
|
|
|
| 1031 |
|
|
\index{debouncing}\index{debouncing!2/3}\emph{2/3 debouncing}
|
| 1032 |
|
|
is debouncing where at least two of the most recent
|
| 1033 |
|
|
three samples must be at the same value (either 0 or 1) to cause the output
|
| 1034 |
|
|
to be that same value.
|
| 1035 |
|
|
|
| 1036 |
|
|
Note that \emph{2/3 debouncing} as we describe it here represents a
|
| 1037 |
|
|
purely combinational mapping from the 3 most recent samples to
|
| 1038 |
|
|
the debounced output. When 3 samples are available, 0 of the
|
| 1039 |
|
|
samples or 1 of the samples with value 1 map to a debounced
|
| 1040 |
|
|
output value of 0; while 2 of the samples or 3 of the samples
|
| 1041 |
|
|
with value 1 map to a debounced output value of 1.
|
| 1042 |
|
|
|
| 1043 |
|
|
If $A$ is the most recent sample, $B$ is the next-most-recent sample, and
|
| 1044 |
|
|
$C$ is the oldest sample, Fig. \ref{fig:cbal0:svct0:sttd0:01}
|
| 1045 |
|
|
supplies the Karnaugh map for 2/3
|
| 1046 |
|
|
debouncing.
|
| 1047 |
|
|
|
| 1048 |
|
|
\begin{figure}
|
| 1049 |
|
|
\centering
|
| 1050 |
|
|
\includegraphics[height=1.25in]{c_bal0/kmap23db.eps}
|
| 1051 |
|
|
\caption{Karnaugh Map Of 2/3 Debouncing}
|
| 1052 |
|
|
\label{fig:cbal0:svct0:sttd0:01}
|
| 1053 |
|
|
\end{figure}
|
| 1054 |
|
|
|
| 1055 |
|
|
It can be seen from the figure that the expression for the output is
|
| 1056 |
|
|
|
| 1057 |
|
|
\begin{equation}
|
| 1058 |
|
|
\label{eq:cbal0:svct0:sttd0:01}
|
| 1059 |
|
|
AB + AC + BC = A (B+C) + BC .
|
| 1060 |
|
|
\end{equation}
|
| 1061 |
|
|
|
| 1062 |
|
|
Intuitively, (\ref{eq:cbal0:svct0:sttd0:01}) makes sense---the output
|
| 1063 |
|
|
will be 1 if any two of the most recent samples are 1
|
| 1064 |
|
|
($AB + AC + BC$). Similarly, the output will be 0 if any two of
|
| 1065 |
|
|
the most recent samples are 0.
|
| 1066 |
|
|
|
| 1067 |
|
|
Figure \ref{fig:cbal0:svct0:sttd0:02} supplies the C-language
|
| 1068 |
|
|
code to implement 2/3 debouncing as a vertical mapping.
|
| 1069 |
|
|
A C-compiler will typically implement this code very directly
|
| 1070 |
|
|
using the bitwise logical instructions of the machine.
|
| 1071 |
|
|
|
| 1072 |
|
|
\begin{figure}
|
| 1073 |
|
|
\begin{verbatim}
|
| 1074 |
|
|
/**************************************************************/
|
| 1075 |
|
|
/* Assume: */
|
| 1076 |
|
|
/* A : Most recent sample (i.e. at t(0)), arranged as */
|
| 1077 |
|
|
/* a group of 8 bits. */
|
| 1078 |
|
|
/* B : Next most recent sample t(-1). */
|
| 1079 |
|
|
/* C : Oldest sample t(-2). */
|
| 1080 |
|
|
/* output : Debounced collection of 8 bits presented to */
|
| 1081 |
|
|
/* software internals. */
|
| 1082 |
|
|
/**************************************************************/
|
| 1083 |
|
|
|
| 1084 |
|
|
output = (A & (B | C)) | (B & C);
|
| 1085 |
|
|
|
| 1086 |
|
|
/* End of code. */
|
| 1087 |
|
|
\end{verbatim}
|
| 1088 |
|
|
\caption{C-Language Implementation Of 2/3 Debouncing}
|
| 1089 |
|
|
\label{fig:cbal0:svct0:sttd0:02}
|
| 1090 |
|
|
\end{figure}
|
| 1091 |
|
|
|
| 1092 |
|
|
\subsection{3/3 Debouncing Vertical Counter}
|
| 1093 |
|
|
%Subsection Tag: TTD1.
|
| 1094 |
|
|
\label{cbal0:svct0:sttd1}
|
| 1095 |
|
|
|
| 1096 |
|
|
\index{debouncing}\index{debouncing!3/3}\emph{3/3 debouncing}
|
| 1097 |
|
|
is debouncing where all three of the most recent
|
| 1098 |
|
|
three samples must be at a value (either 0 or 1) to cause the
|
| 1099 |
|
|
debounced output to transition to that same value.
|
| 1100 |
|
|
|
| 1101 |
|
|
Note that 3/3 debouncing as we present it is a sequential (rather than
|
| 1102 |
|
|
a purely combinational) mapping from the 3 most recent samples to the
|
| 1103 |
|
|
debounced output. In addition to the 3 inputs, the behavior of the
|
| 1104 |
|
|
mapping depends on a single bit of state which is held. (In the
|
| 1105 |
|
|
implementation presented in this section, the state and the debounced
|
| 1106 |
|
|
output are the same bit.) For example, if 2 of the 3 most recent
|
| 1107 |
|
|
input samples are 1, the debounced output value may be either 0
|
| 1108 |
|
|
or 1. The transition of the debounced output value from
|
| 1109 |
|
|
0 to 1 or from 1 to 0 can only occur if all 3 most recent samples
|
| 1110 |
|
|
are 1 or are 0, respectively.
|
| 1111 |
|
|
|
| 1112 |
|
|
If $A$ is the most recent sample, $B$ is the next-most-recent sample,
|
| 1113 |
|
|
$C$ is the oldest sample, and $O$ is the output (assumed maintained
|
| 1114 |
|
|
as a RAM location) Fig. \ref{fig:cbal0:svct0:sttd1:01}
|
| 1115 |
|
|
supplies the Karnaugh map for 3/3
|
| 1116 |
|
|
debouncing.
|
| 1117 |
|
|
|
| 1118 |
|
|
\begin{figure}
|
| 1119 |
|
|
\centering
|
| 1120 |
|
|
\includegraphics[height=2.0in]{c_bal0/kmap33db.eps}
|
| 1121 |
|
|
\caption{Karnaugh Map Of 3/3 Debouncing}
|
| 1122 |
|
|
\label{fig:cbal0:svct0:sttd1:01}
|
| 1123 |
|
|
\end{figure}
|
| 1124 |
|
|
|
| 1125 |
|
|
It can be seen from the figure that the expression for the output is
|
| 1126 |
|
|
|
| 1127 |
|
|
\begin{equation}
|
| 1128 |
|
|
\label{eq:cbal0:svct0:sttd1:01}
|
| 1129 |
|
|
ABC + AO + BO + CO = ABC + O(A + B + C).
|
| 1130 |
|
|
\end{equation}
|
| 1131 |
|
|
|
| 1132 |
|
|
Intuitively, (\ref{eq:cbal0:svct0:sttd1:01}) makes sense---the output
|
| 1133 |
|
|
will be unconditionally 1 if all three of the most recent samples are 1
|
| 1134 |
|
|
($ABC$). The output will also be 1 if the previous output was 1
|
| 1135 |
|
|
and at least one of the most recent samples are 1 [$O(A+B+C)$]---at least
|
| 1136 |
|
|
one true recent sample blocks the output from transition to 0.
|
| 1137 |
|
|
|
| 1138 |
|
|
Figure \ref{fig:cbal0:svct0:sttd1:02} supplies the C-language
|
| 1139 |
|
|
code to implement 3/3 debouncing as a vertical mapping.
|
| 1140 |
|
|
A C-compiler will typically implement this code very directly
|
| 1141 |
|
|
using the bitwise logical instructions of the machine.
|
| 1142 |
|
|
|
| 1143 |
|
|
\begin{figure}
|
| 1144 |
|
|
\begin{verbatim}
|
| 1145 |
|
|
/**************************************************************/
|
| 1146 |
|
|
/* Assume: */
|
| 1147 |
|
|
/* A : Most recent sample (i.e. at t(0)), arranged as */
|
| 1148 |
|
|
/* a group of 8 bits. */
|
| 1149 |
|
|
/* B : Next most recent sample t(-1). */
|
| 1150 |
|
|
/* C : Oldest sample t(-2). */
|
| 1151 |
|
|
/* output : Debounced collection of 8 bits presented to */
|
| 1152 |
|
|
/* software internals. Note that this is both */
|
| 1153 |
|
|
/* an input (to the combinational mapping) and */
|
| 1154 |
|
|
/* the new result. */
|
| 1155 |
|
|
/**************************************************************/
|
| 1156 |
|
|
|
| 1157 |
|
|
output = (A & B & C) | (output & (A | B | C));
|
| 1158 |
|
|
|
| 1159 |
|
|
/* End of code. */
|
| 1160 |
|
|
\end{verbatim}
|
| 1161 |
|
|
\caption{C-Language Implementation Of 3/3 Debouncing}
|
| 1162 |
|
|
\label{fig:cbal0:svct0:sttd1:02}
|
| 1163 |
|
|
\end{figure}
|
| 1164 |
|
|
|
| 1165 |
|
|
\subsection{N/N Debouncing Vertical Counter}
|
| 1166 |
|
|
%Subsection Tag: NNC0.
|
| 1167 |
|
|
\label{cbal0:svct0:snnc0}
|
| 1168 |
|
|
|
| 1169 |
|
|
\index{debouncing}\index{debouncing!N/N}It is clear from
|
| 1170 |
|
|
the design of the 3/3 debouncing
|
| 1171 |
|
|
vertical counter (Section \ref{cbal0:svct0:sttd1}, immediately
|
| 1172 |
|
|
above) that the design of the 3/3 debouncing vertical counter
|
| 1173 |
|
|
can be generalized to cover any number of recent samples.
|
| 1174 |
|
|
We call such a debouncing vertical counter an N/N debouncing
|
| 1175 |
|
|
vertical counter. In order for the output of such a counter to
|
| 1176 |
|
|
turn 1, all $N$ most recent samples must be 1. Similarly, in order
|
| 1177 |
|
|
for such a counter to turn 0, all $N$ most recent samples must be 0.
|
| 1178 |
|
|
|
| 1179 |
|
|
We rely on a logical argument to design such a N/N debouncing
|
| 1180 |
|
|
vertical counter, rather than on Karnaugh maps. If $I_1 \ldots I_N$
|
| 1181 |
|
|
are the $N$ most recent input samples and $O$ is the most recent
|
| 1182 |
|
|
output (assumed stored in RAM), it is clear from the form of
|
| 1183 |
|
|
(\ref{eq:cbal0:svct0:sttd1:01}) that the formula for the new output
|
| 1184 |
|
|
as a function of the inputs $I_1 \ldots I_N$ and the
|
| 1185 |
|
|
most recent output $O_{k-1}$ must be:
|
| 1186 |
|
|
|
| 1187 |
|
|
\begin{equation}
|
| 1188 |
|
|
\label{eq:cbal0:svct0:snnc0:01}
|
| 1189 |
|
|
O_k = I_1 I_2 \ldots I_N + (O_{k-1} (I_1 + I_2 + \ldots + I_N)) .
|
| 1190 |
|
|
\end{equation}
|
| 1191 |
|
|
|
| 1192 |
|
|
The form of (\ref{eq:cbal0:svct0:snnc0:01}) is intuitively
|
| 1193 |
|
|
plausible. If the previous output $O_{k-1}$ is 0, the only
|
| 1194 |
|
|
circumstance under which the next output $O_k$ will become 1
|
| 1195 |
|
|
is if all $N$ inputs $I_1, I_2, \ldots , I_N$ are 1.
|
| 1196 |
|
|
Similarly, if the previous output $O_{k-1}$ is 1, the only
|
| 1197 |
|
|
circumstance under which $O_k$ will become 0
|
| 1198 |
|
|
is if all $N$ inputs $I_1, I_2, \ldots , I_N$ are 0. This
|
| 1199 |
|
|
is the desired behavior.
|
| 1200 |
|
|
|
| 1201 |
|
|
For an N/N counter when a large number of previous samples
|
| 1202 |
|
|
are required to be at the same value (say, $N=10$, for example),
|
| 1203 |
|
|
it may seem that the efficiency of the N/N vertical counter
|
| 1204 |
|
|
design presented here will break down. However, it must be
|
| 1205 |
|
|
remembered that the vertical counter approach manipulates
|
| 1206 |
|
|
a large number (usually 8 or 16) inputs at a time. It can be
|
| 1207 |
|
|
shown easily that an N/N debouncing vertical counter requires
|
| 1208 |
|
|
$2N$ operations to determine the next output. Thus, for a
|
| 1209 |
|
|
10/10 debouncing vertical counter, the necessary software
|
| 1210 |
|
|
may execute in as little as 20 machine instructions. It would
|
| 1211 |
|
|
be difficult to find another method which will perform 10/10
|
| 1212 |
|
|
debouncing for 8 or 16 inputs in only 20 machine instructions, thus
|
| 1213 |
|
|
we maintain that the N/N debouncing vertical counter
|
| 1214 |
|
|
approach presented is quite efficient even for larger
|
| 1215 |
|
|
$N$.
|
| 1216 |
|
|
|
| 1217 |
|
|
|
| 1218 |
|
|
\section{Authors And Acknowledgements}
|
| 1219 |
|
|
%Section tag: ACK0
|
| 1220 |
|
|
This chapter was primarily written by David T. Ashley
|
| 1221 |
|
|
\cite{bibref:i:daveashley}.
|
| 1222 |
|
|
|
| 1223 |
|
|
We are very grateful to \index{Dattalo, Scott}Scott Dattalo
|
| 1224 |
|
|
\cite{bibref:i:scottdattalo},
|
| 1225 |
|
|
whose web pages about vertical counters provided much of the
|
| 1226 |
|
|
material for the Section \ref{cbal0:svct0}.
|
| 1227 |
|
|
Special thanks to \index{Virgil}Virgil \cite{bibref:i:virgil},
|
| 1228 |
|
|
\index{Dresner, Norm}Norm Dresner \cite{bibref:i:normdresner},
|
| 1229 |
|
|
and \index{Kaskelma, Heikki}Heikki Kaskelma \cite{bibref:i:heikkikaskelma}
|
| 1230 |
|
|
for mathematical assistance provided via the
|
| 1231 |
|
|
\index{sci.math newsgroup@\texttt{sci.math} newsgroup}%
|
| 1232 |
|
|
\texttt{sci.math} \cite{bibref:n:scimathnewsgroup} newsgroup.
|
| 1233 |
|
|
|
| 1234 |
|
|
|
| 1235 |
|
|
\section{Exercises}
|
| 1236 |
|
|
|
| 1237 |
|
|
|
| 1238 |
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
| 1239 |
|
|
|
| 1240 |
|
|
\noindent\begin{figure}[!b]
|
| 1241 |
|
|
\noindent\rule[-0.25in]{\textwidth}{1pt}
|
| 1242 |
|
|
\begin{tiny}
|
| 1243 |
|
|
\begin{verbatim}
|
| 1244 |
|
|
$RCSfile: c_bal0.tex,v $
|
| 1245 |
|
|
$Source: /home/dashley/cvsrep/e3ft_gpl01/e3ft_gpl01/dtaipubs/esrgubka/c_bal0/c_bal0.tex,v $
|
| 1246 |
|
|
$Revision: 1.10 $
|
| 1247 |
|
|
$Author: dtashley $
|
| 1248 |
|
|
$Date: 2003/11/03 02:14:24 $
|
| 1249 |
|
|
\end{verbatim}
|
| 1250 |
|
|
\end{tiny}
|
| 1251 |
|
|
\noindent\rule[0.25in]{\textwidth}{1pt}
|
| 1252 |
|
|
\end{figure}
|
| 1253 |
|
|
|
| 1254 |
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
| 1255 |
|
|
% $Log: c_bal0.tex,v $
|
| 1256 |
|
|
% Revision 1.10 2003/11/03 02:14:24 dtashley
|
| 1257 |
|
|
% All duplicate labels as flagged by LaTeX removed. Additional files added
|
| 1258 |
|
|
% to Microsoft Visual Studio edit context.
|
| 1259 |
|
|
%
|
| 1260 |
|
|
% Revision 1.9 2001/07/11 18:42:04 dtashley
|
| 1261 |
|
|
% Safety check-in. Beginning work now on using GNU GMP in the tool set
|
| 1262 |
|
|
% and must cease work on book temporarily.
|
| 1263 |
|
|
%
|
| 1264 |
|
|
% Revision 1.8 2001/07/09 22:44:36 dtashley
|
| 1265 |
|
|
% All figures changed to use the Courier font. Full checkin of this
|
| 1266 |
|
|
% subdirectory after this change. Reason for font change was font
|
| 1267 |
|
|
% substitution warning messages both during print from 4AllTeX and from Acrobat
|
| 1268 |
|
|
% Distiller.
|
| 1269 |
|
|
%
|
| 1270 |
|
|
% Revision 1.7 2001/07/09 02:22:55 dtashley
|
| 1271 |
|
|
% Edits. Safety check-in after changes and addition of figures.
|
| 1272 |
|
|
%
|
| 1273 |
|
|
% Revision 1.6 2001/07/07 03:19:52 dtashley
|
| 1274 |
|
|
% Test commit to be sure the CVS add worked correctly in adding files.
|
| 1275 |
|
|
%
|
| 1276 |
|
|
% Revision 1.5 2001/07/06 23:46:53 dtashley
|
| 1277 |
|
|
% Edits. Addition of K-map diagrams to Boolean function chapter.
|
| 1278 |
|
|
%
|
| 1279 |
|
|
% Revision 1.4 2001/07/01 21:10:59 dtashley
|
| 1280 |
|
|
% Safety check-in after major re-org.
|
| 1281 |
|
|
%
|
| 1282 |
|
|
% Revision 1.3 2001/06/30 23:32:07 dtashley
|
| 1283 |
|
|
% End-of-month safety check-in.
|
| 1284 |
|
|
%
|
| 1285 |
|
|
% Revision 1.2 2001/06/30 16:32:10 dtashley
|
| 1286 |
|
|
% Moved out of binary mode for use of CVS.
|
| 1287 |
|
|
%
|
| 1288 |
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
| 1289 |
|
|
% $History: c_bal0.tex $
|
| 1290 |
|
|
%
|
| 1291 |
|
|
% ***************** Version 3 *****************
|
| 1292 |
|
|
% User: Dashley1 Date: 12/22/00 Time: 12:53a
|
| 1293 |
|
|
% Updated in $/uC Software Multi-Volume Book (A)/Chapter, BAL0, Bolean Algebra
|
| 1294 |
|
|
% Tcl build is up and running. Result is near-perfect.
|
| 1295 |
|
|
%
|
| 1296 |
|
|
% ***************** Version 2 *****************
|
| 1297 |
|
|
% User: David T. Ashley Date: 7/09/00 Time: 11:15p
|
| 1298 |
|
|
% Updated in $/uC Software Multi-Volume Book (A)/Chapter, BAL0, Bolean Algebra
|
| 1299 |
|
|
% Addition of new chapters, enhancements to preface.
|
| 1300 |
|
|
%
|
| 1301 |
|
|
% ***************** Version 1 *****************
|
| 1302 |
|
|
% User: David T. Ashley Date: 7/09/00 Time: 9:28p
|
| 1303 |
|
|
% Created in $/uC Software Multi-Volume Book (A)/Chapter, BAL0, Bolean Algebra
|
| 1304 |
|
|
% Initial check-in.
|
| 1305 |
|
|
%End of file C_BAL0.TEX
|

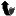 Parent Directory
|
Parent Directory
|  Revision Log
Revision Log